All chlorophyll-containing organisms in the ocean, through the process of photosynthesis, convert energy from the sunlight and carbon dioxide into the organic material. Some of that carbon is used for cellular upkeep and the remaining portion of the carbon is what makes Net Primary Production (NPP). This proportion of phytoplankton-sequestered carbon is available to enter into the trophic cascades of the oceanic food web and continues its path through the biological carbon pump.
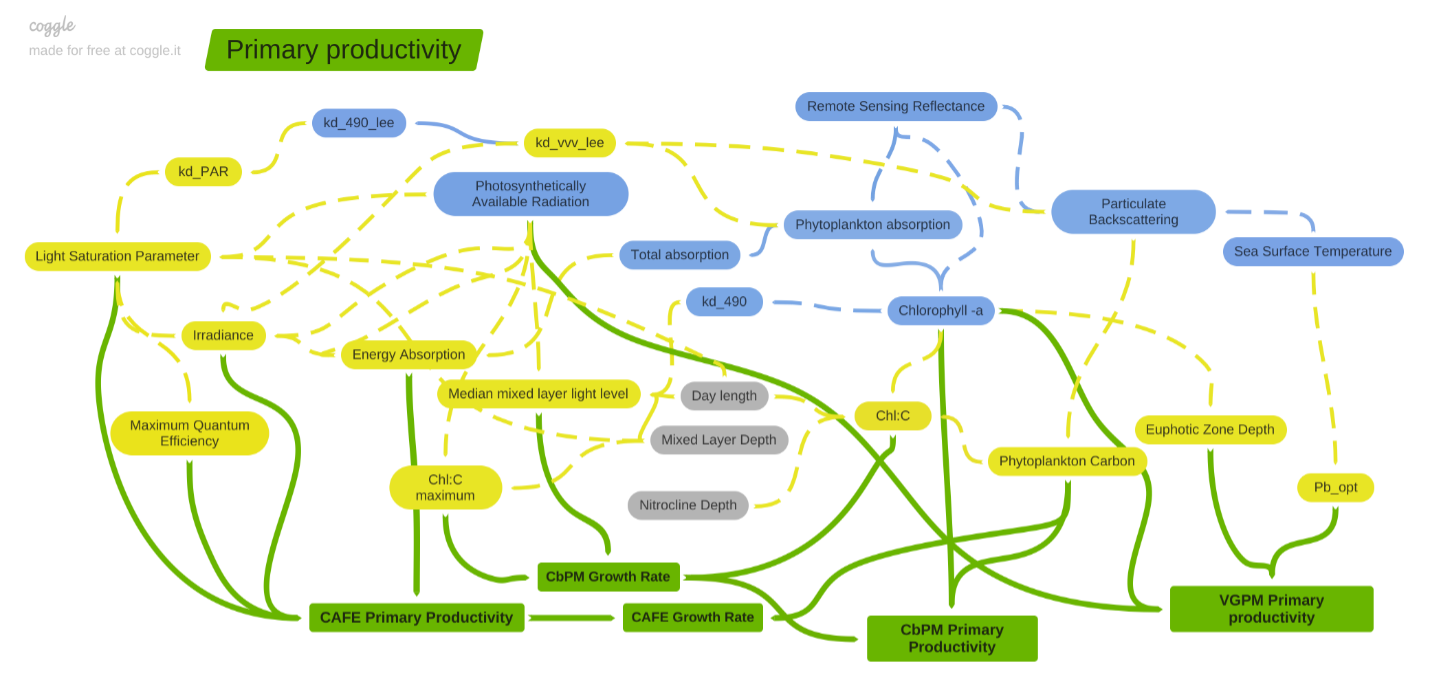
The Vertically Generalized Production Model (VGPM) is a chlorophyll-based approach for derivation of the global oceanic NPP (Behrenfeld and Falkowski 1997). It relies on the assumption that NPP is a function of chlorophyll, moderated by the available light within the euphotic zone, and that the maximum photosynthetic efficiency (Pb_opt) is dependent on the sea surface temperature (SST). In the standard VGPM, the modeled Pb_opt reflects nutrient-stress effects at high SST (i.e. decreasing photosynthetic efficiency at high (> 20°C) temperatures), while VGPM-Eppley assumes that higher temperature/higher PAR conditions favor high-light acclimated phytoplankton, which require less chlorophyll to support photosynthetic requirements for growth. Thus Pb_opt increases continuously as temperature increases throughout the full range of SST, see Eppley (1972).
Inputs:
chlor_a, concentration of Chlorophyll a, in mg m-3
PAR, Photosynthetically available radiation, in Einsteins per day per square meter
SST, sea surface temperature, in °C
dayL, length of day, in decimal hours
Outputs:
npp, net primary productivity, in mg C m-2 day-1
The Carbon-based Productivity Model (CbPM) is a spectrally-resolved, depth-resolved approach for derivation of the global oceanic NPP (Behrenfeld et al. (2005), Westberry et al. (2008)). In contrast to the empirical VGPM approaches, the CbPM estimates NPP as a function of phytoplankton carbon biomass (Cphyto; derived from particulate backscatter coefficients; Behrenfeld et al. 2005) and growth rate ($\mu$; estimated from satellite-derived chlorophyll-to-carbon [Chl:C] ratios). The theoretical maximum growth rate ($\mu$max = 2 divisions/day) is dynamically adjusted according to varying mixed layer light conditions (Ig; derived from MLD, PAR, and KPAR) to account for impacts of nutrient and temperature stress [f(N,T)] on the Chl:C ratio in addition to correcting for the suppression of growth rate due to light limitation [i.e. growth irradiance; g(Ig)]. The Chl:C ratio is additionally modified by how much the depth of interest exceeds the depth of the nitricline (zno3; obtained from World Ocean Atlas). The CbPM is fundamentally different from chlorophyll-based models in that is attempts to reduce uncertainty in assumptions of physiological variability by incorporating light and nutrient impacts on phytoplankton pigmentation levels.
Inputs:
chlor_a, concentration of Chlorophyll a, in mg m-3
bbp, GIOP particulate backscattering, m-1
PAR, Photosynthetically available radiation, in Einsteins per day per square meter
kd490, diffuse attenuation coefficient at 490 nm, m-1
dayL, length of day, in decimal hours
mld, mixed layer depth (HYCOM, 1°), in m
zno3, nitricline, defined as depth where [NO3-] < 0.5 uM (World Ocean Atlas)
Outputs:
npp, net primary productivity, in mg C m-2 day-1
μ, growth rate, in day-1
The Carbon, Absorption, and Fluorescence Euphotic-resolving (CAFE) model is a mechanistic depth-resolved, spectrally-resolved, and time-resolved approach for the derivation of the global oceanic NPP and phytoplankton growth rates ($\mu$). This absorption-based model exploits advances in ocean color inversion algorithms to define the inherent optical properties (IOPs) of the water, and thus defines NPP as a product of energy absorption (QPAR; derived from irradiance and the sum of phytoplankton absorption, af, relative to total absorption) and the quantum efficiency of growth ($\phi_\mu$; adjusted as a function of irradiance and the light saturation parameter, Ek). The Ek model is based on fundamental principles of pigment synthesis regulation (Behrenfeld et al. 2016), and the derivation incorporates changes in spectral quality with depth/absorbed energy (Markager and Vincent 2001), and dynamically adjusts for bulk photoacclimatory status depending on the ratio of mixed layer depth (MLD) to the euphotic depth (Zeu). Absorption-based models are advantageous in that they encapsulate accessory-pigment composition, and hold a direct relation to radiance observed from satellites.
Input:
chlor_a, concentration of Chlorophyll a, in mg m-3
SST, sea surface temperature, in °C
PAR, Photosynthetically available radiation, in Einsteins per day per square meter
adg, GIOP detrital/gelbstoff absorption, m-1 (Werdell et al. 2013)
aph, GIOP phytoplankton absorption, m-1
bbp, GIOP particulate backscattering, m-1
bbps, GIOP particulate backscattering slope, m-1
mld, mixed layer depth (HYCOM, 1°), in m
dayL, length of day, in decimal hours
Outputs:
npp, net primary productivity, in mg C m-2 day -1
μ, growth rate, in day-1
The IOP model and phytoplankton carbon product utilized in the npp model may be modified as follows (applicable to npp_cbpm and npp_cafe):
iop_opt (int) (default=7) = IOP model for use in downstream products
cphyt_opt (int) (default=1) = phytoplankton carbon (c_phyt) product
Several Primary Production Algorithm Round Robin (PPARR) studies have assessed the skill and sensitivity of NPP models (Campbell et al. 2002, Carr et al. 2006, Saba et al. 2011, Lee et al. 2015). In the PPARR studies, input data (e.g. chlorophyll, SST, PAR, and mixed layer depth for specific locations and dates) are provided by the organizers to the participating modeling groups, who in turn estimate integrated primary productivity. These results are sent back to the organizers, who compare and analyze the results in relation to direct field measurements. The model performance is quantified by assessing the Root Mean Square Difference (RMSD) and mean bias between the modeled NPP v. observed NPP. Results from VGPM, CbPM, and CAFE model validation for 8 different oceanic subregions, as well as two time-series sites (HOTS and BATS) are presented in Silsbe (2016).
Behrenfeld, M. J., & Falkowski, P. G. (1997). Photosynthetic rates derived from satellite‐based chlorophyll concentration. Limnology and oceanography, 42(1), 1-20.
Behrenfeld, M. J., Boss, E., Siegel, D. A., & Shea, D. M. (2005). Carbon‐based ocean productivity and phytoplankton physiology from space. Global biogeochemical cycles, 19(1).
Behrenfeld, M. J., O’Malley, R. T., Boss, E. S., Westberry, T. K., Graff, J. R., Halsey, K. H., etc. & Brown, M. B. (2016). Revaluating ocean warming impacts on global phytoplankton. Nature Climate Change, 6(3), 323-330.
Campbell, J., Antoine, D., Armstrong, R., Arrigo, K., Balch, W., Barber, R., etc. & Esaias, W. (2002). Comparison of algorithms for estimating ocean primary production from surface chlorophyll, temperature, and irradiance. Global biogeochemical cycles, 16(3), 9-1.
Carr, M. E., Friedrichs, M. A., Schmeltz, M., Aita, M. N., Antoine, D., Arrigo, K. R., etc. & Bidigare, R. (2006). A comparison of global estimates of marine primary production from ocean color. Deep Sea Research Part II: Topical Studies in Oceanography, 53(5-7), 741-770.
Eppley, R. W. (1972). Temperature and phytoplankton growth in the sea. Fish. bull, 70(4), 1063-1085.
Graff, J.R., Westberry, T.K., Milligan, A.J., Brown, M.B., Dall’Olmo, G., Dongen-Vogels, V.v., Reifel, K.M., & Behrenfeld, M.J. (2015). Analytical phytoplankton carbon measurements spanning diverse ecosystems. Deep Sea Research Part I: Oceanographic Research Papers, 102, 16-25
Lee, Y. J., Matrai, P. A., Friedrichs, M. A., Saba, V. S., Antoine, D., Ardyna, M., ... & Devred, E. (2015). An assessment of phytoplankton primary productivity in the Arctic Ocean from satellite ocean color/in situ chlorophyll‐a based models. Journal of Geophysical Research: Oceans, 120(9), 6508-6541.
Markager, S., & Vincent, W. F. (2001). Light absorption by phytoplankton: development of a matching parameter for algal photosynthesis under different spectral regimes. Journal of Plankton Research, 23(12), 1373-1384.
Saba, V. S., Friedrichs, M. A., Antoine, D., Armstrong, R. A., Asanuma, I., Behrenfeld, M. J., ... & Ishizaka, J. (2011). An evaluation of ocean color model estimates of marine primary productivity in coastal and pelagic regions across the globe. Biogeosciences, 489-503.
Silsbe, G. M., Behrenfeld, M. J., Halsey, K. H., Milligan, A. J., & Westberry, T. K. (2016). The CAFE model: A net production model for global ocean phytoplankton. Global Biogeochemical Cycles, 30(12), 1756-1777.
Werdell, P. J., Franz, B. A., Bailey, S. W., Feldman, G. C., Boss, E., Brando, V. E., ... & Loisel, H. (2013). Generalized ocean color inversion model for retrieving marine inherent optical properties. Applied optics, 52(10), 2019-2037.
Westberry, T., Behrenfeld, M. J., Siegel, D. A., & Boss, E. (2008). Carbon‐based primary productivity modeling with vertically resolved photoacclimation. Global Biogeochemical Cycles, 22(2).
TBD