This algorithm returns the skin sea surface temperature in units of °C using the 3.7 μm, 11 μm and 12 μm mid- and long-wave infrared bands and is applicable to the VIIRS sensor and night time observations only.
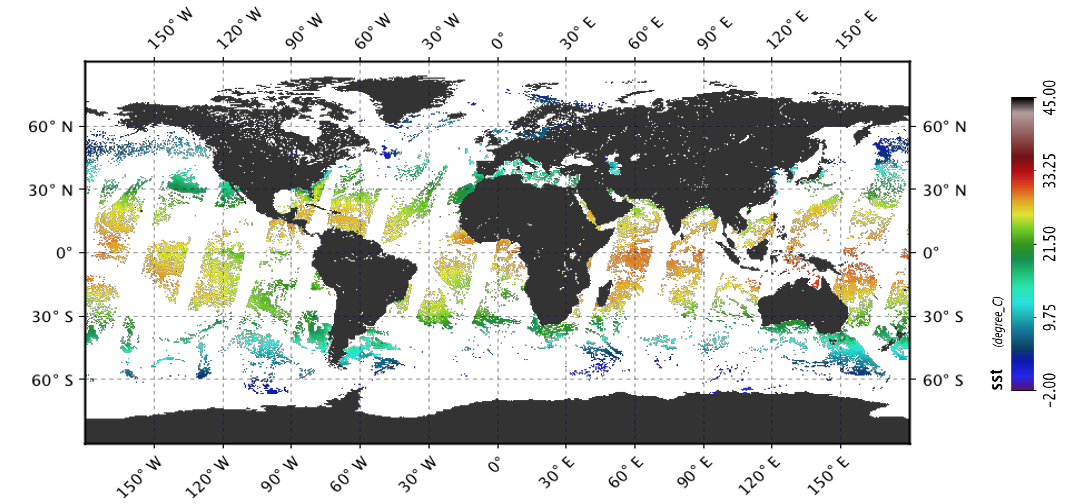
Algorithm point of contact: Peter Minnett of the Rosenstiel School of Marine and Atmospheric Science (RSMAS) at the University of Miami.
NASA standard processing and distribution of the Sea Surface Temperature (SST) products from MODIS and VIIRS sensors are performed using software developed by the Ocean Biology Processing Group (OBPG). The OBPG generates Level-2 SST products using the Multi-Sensor Level-1 to Level-2 software (l2gen), which is the same software used to generate MODIS and VIIRS ocean color products. The SST algorithm and quality assessment logic are the responsibility of the MODIS and VIIRS Science Team Lead for SST (P. Minnett currently for MODIS and up to summer 2018 for VIIRS). The TOA brightness temperatures used by the SST algorithm are derived from the measured calibrated radiances using Planck’s Equation convolved with the spectral response function of each band. To facilitate processing directly from the L1a files, and eliminate the need to archive the L1b at the OB.DAAC, l2gen uses a radiance to brightness temperature relationship table that is precomputed for the spectral response of each channel. These precomputed tables have been verified to produce identical brightness temperatures to those found in the standard L1b files and are stored locally and loaded during L2 processing at runtime.
Details of the SST processing implementation within l2gen are provided in this document. The description is valid for both the NASA standard products distributed by the Ocean biology DAAC (OB.DAAC) through the ocean color web and the products delivered to the Physical Oceanography DAAC, where the latter are subsequently repackaged for the Group for High Resolution SST (GHRSST) distribution in L2p format.
The sea surface temperature derived from measurements of MODIS and VIIRS infrared radiometers is commonly referred to as the skin temperature of the ocean. This is because the radiance measured by infrared radiometers originates in the surface thermal skin layer of the ocean and not the body of water below, often referred to as the temperature at depth, as measured by in situ thermometers. The surface skin layer of the ocean is less than 1mm thick (Hanafin, 2002; Hanafin and Minnett, 2003; Wong and Minnett, 2016; Wong and Minnett, 2018) and as a rule will be cooler than the underlying water due to heat flux, with the direction of flux typically from the ocean to the atmosphere. Three distinct processes impact near surface ocean temperature gradients: absorption of solar isolation, heat exchange with the atmosphere, and sub-surface turbulence. Generally, at night or when wind speeds are > ~6 m/s the relationship between the skin temperature and the subsurface is often quite stable (Donlon et al., 2002; Minnett et al., 2011). It is under these conditions that validation and uncertainty estimates relative to subsurface in situ buoys are typically reported. The relationship can however be very variable under conditions of high insolation, low wind speeds, and reduced sub-surface turbulence. A more complete discussion of subsurface SST gradients and $SST_{depth}$ definitions and applications can be found here. The challenge of validating satellite $SST_{skin}$ retrievals for a climate data record, and the use of ship board radiometers for validation, can be found in Minnett (2010) and Minnett and Corlett (2012).
The night time only $SST_{triple}$ algorithm is based on a modified version of the nonlinear multi-channel SST algorithm of Walton et, al, (1998) and uses empirical coefficients derived by regression of collocated in situ and satellite observations. The $SST_{triple}$ products currently available from VIIRS (R2016.0) use month-of-year coefficients derived for six distinct atmospheric regions based on latitude. The equivalent MODIS night-time only SST4 algorithm, is based on measurements close to λ = 4 μm and can be found here. However, the spectrally narrow MODIS bands at λ = 3.95 μm and 4.05 μm are missing from VIIRS and so an algorithm applicable to nighttime measurements for VIIRS band at λ = 3.7 μm, 11 μm,12 μm is used.
The base SSTtriple algorithm form, shown in the next section in black, was developed to generate night time NOAA AVHRR SST products. To extend the NLSST algorithm for optimum performance with the modern sensor design characteristics of VIIRS, three additional algorithm terms (in red) were added to the base formulation. These new terms are related to (i) correcting for any potential imbalance between mirror sides, (ii) reducing any response versus scan angle (RVS) issues that may be present due to uncharacterized changes or degradation in mirror surfaces, and (iii) improving retrievals at the increasingly longer path-length of MODIS and VIIRS.
The current algorithm for computing SST from observed MWIR and LWIR brightness temperatures is shown below.
The coefficients aj are derived and continuously verified using match-ups between the satellite measurements of brightness temperature and field measurements of sea surface temperature. As currently implemented, these coefficients are time-dependent as month-of-year. The coefficients are provided to l2gen through external files, which are in a columned ascii format of "sensor start-date, end-date, latitude start, latitude end, $ai_{0}, ai_{1}, ai_{2}, ai_{3}, ai_{4}, ai_{5}, ai_{6}$". Coefficients are sensor-dependent. A link to the $SST_{triple}$ coefficient file is here.
For R2019 MODIS and R2016.2 VIIRS the $T_{sfc}$ reference product was changed to be the Canadian Meteorological Center Global Foundation Sea Surface temperature product (CMCSST; Brasnett B., 2008), due to degradation and calibration issues of several of the more recent AVHRR sensors used in the NOAA OI SST and loss of in situ observations (Liu et. al. 2019). Changing to the CMCSST reference field has no significant statistical impact on the uncertainty in the NASA SST products (see assessment section below). The purpose of the $T_{sfc}$ reference, in the second term of the atmospheric correction algorithm, acts as a weighting factor for the magnitude of the correction contributed by the BT difference. At warm sea surface temperatures, the top of the atmosphere (TOA) temperature deficit in the 11µm band increases due to increased water vapor absorption. At the equator this deficit may be up to 8 degrees. In contrast at the high latitudes the TOA deficit for a cold surface under a dry atmosphere may be less than 1 degree for a similar BT difference. The BT differences in Arctic atmospheres is not a simple linear function of only water vapor, but other atmospheric components can play a role including the orientation of ice crystal aerosols (Vincent et al. 2008a, 2008b; Vincent 2019), and differences in surface emissivity which become more important for very dry atmospheres (Jia, 2019). The use of a $T_{sfc}$ reference weights the magnitude of the correction in the second term of the as a function of the nominal surface temperature, and is greatest for warm temperatures typically characterized by high water vapor in the overlying atmosphere.
Coefficient sets are currently supplied as a function of month (i) and latitude band (j or k). To reduce the potential for discontinuity at geographic boundaries, when switching between sets of coefficients, the SST of a pixel within ± 2.5° latitude of a boundary are weighted as a function of geographic distance from the transition according to the following formulation.
$$ SST_{lo} = aij_{0} +aij_{1}T_{11μm} + aij_{2}(T_{3.7μm}-T_{12μm}) T_{sfc} + aij_{3}(sec(θ)-1) + aij_{4}(mirror) + aij_{5}(θ^*) +aij_{6}(θ^2) $$ $$ SST_{hi} = aijk_{0} +aik_{1}T_{11μm} + aik_{2}(T_{3.7μm}-T_{12μm}) T_{sfc} + aik_{3}(sec(θ)-1) + aik_{4}(mirror) + aik_{5}(θ^*) +aik_{6}(θ^2) $$ $$ SST_{sat} = SST_{lo} + (lat – jlat +2.5) * (SST_{hi} - SST_{lo}) / 5.0 $$All OB.DAAC files contain a numeric Quality Level for each pixel, assigned by a evaluating a set of tests stored in SST_flags, with quality level 0 being the highest quality and quality 4 being the worst. Clear data assigned the highest quality is limited to satellite zenith angles that are between 0o and 55°, where the atmospheric path length is shorter and where error characteristics are better characterized and generally stable and predictable. Clear pixels with satellite angles > 55° are assigned to good quality 1 and are useable, but may have higher inaccuracies. Quality levels > 1 should not be used for scientific studies as they may have significant cloud contamination or a variety of other problems.
| Quality Level | Meaning |
|---|---|
| 0 | Best satellite zenith angles < 55° |
| 1 | Good/acceptable in glint or high scan angle |
| 2 | Suspect |
| 3 | Bad Cloud/ice/or atmospheric correction failed |
| 4 | Not processed or land |
Note: For PO.DAAC L2p GHRSST formatted files the quality/proximity confidence value order is reversed, with 5 “best” and 4 “good” being useable retrievals. Any L2p quality values < 3 are unacceptable for the NASA SST products described here and should not be used for scientific purposes.
VIIRS uses a cloud classification scheme based on the theory of Alternating Decision Trees (ADtree) developed by Freund and Mason (1999) and modified by Pfahringer et. al. (2000). The VIIRS ADtree classifier (Kilpatrick et. al., 2019) is an ensemble collection of both weak and strong classifiers with multiple binary decision nodes each ending with a prediction node containing a vote. Each vote is scaled by the predictive power of the test and the votes from all true nodes are summed. The magnitude of the summed vote therefore provides an indication of the confidence of the classification. The advantage of using an ADtree classifier is that the combined votes from a collection of weak prediction nodes when voting together as a block can modify or override the vote of a single strong prediction node. When the training of an ADtree classifier is also combined with a boosting algorithms, where at each iteration during training the instances that were previously misclassified are pooled together, a very accurate ensemble classification model is possible.
The ADtree classifier was trained to classify both the night time VIIRS SST and $SST_{triple}$ retrievals as clear or cloudy using a subset of the VIIRS buoy Matchup Database (MUDB). The classification model was validated on independent subsets of the VIIRS MUDB. For the night ADtree classifier we show the nested tests and the vote for each individual test. If a test is true, the value after the colon is added to the running sum and forms the cumulative vote for a pixel. The sign of the vote indicates the predicted Class: negative is cloudy and positive is clear. The absolute value of the magnitude of the vote indicates the confidence of the prediction for the Class.
SST products are validated using a matchup data base (MUDB) of in situ observations that are collected within 30 minutes of an overpass and at least 10 km of a pixel. The in situ data sources include both sub-surface in situ observations from drifting and fixed buoys from the IQUAM database (Xu & Ignatov, 2014), and direct measurements of ocean skin temperatures from ship board Marine-Atmospheric Emitted Radiance Interferometer (M-AERI; Minnett el a. 2001) and Infrared Sea surface temperature Autonomous Radiometer (ISAR; Donlon et al., 2008). The M-AERI and ISAR validation provides SI traceability to standards at NIST (National Institute of Standards and Technology; Rice et al. 2004) and NPL (National Physical Laboratory, UK; Theocharous et al., 2019). However, the quantity and geographical coverage of radiometer $SST_{skin}$ measurements are significantly limited compared to the large network of buoy observations, but which have a larger calibration uncertainty.
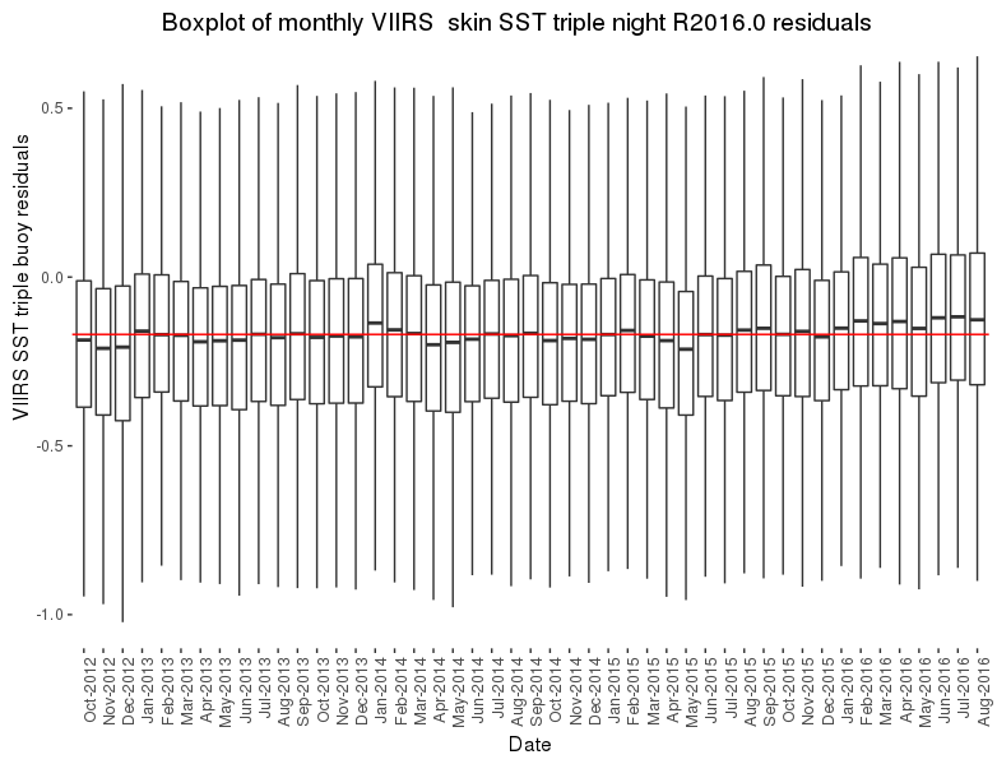
| Sensor | quality | mean | median | SD | RSD | Count |
|---|---|---|---|---|---|---|
| VIIRS skin $SST_{triple}$ – sub-surface buoy SST | ||||||
| VIIRS $SST_{triple}$ | 0 | -0.145 | -0.143 | 0.349 | 0.173 | 399094 |
| VIIRS $SST_{triple}$ | 1 | -0.247 | -0.219 | 0.499 | 0.242 | 287638 |
| Sensor | quality | mean | median | SD | RSD | Count |
|---|---|---|---|---|---|---|
| VIIRS skin $SST_{triple}$ – radiometer $SST_{skin}$. R/V Alliance, M-AERI unit A | ||||||
| VIIRS $SST_{triple}$ | 0 | -0.076 | -0.040 | 0.179 | 0.141 | 73 |
| VIIRS $SST_{triple}$ | 1 | -0.016 | 0.073 | 0.265 | 0.195 | 38 |

Brasnett B., (2008). The impact of satellite retrievals in a global sea-surface-temperature analysis. Q.J.R. Meteorol. Soc., 134, 1745-1760. DOI: 10.1002/qj.319
Brown, O.B. & Minnett, P.J. (1999). MODIS Infrared Sea Surface Temperature Algorithm — Algorithm Theoretical Basis Document. University of Miami. 91 pp. Available from http://oceancolor.gsfc.nasa.gov/cmsdocs/technical_documents/atbd_mod25.pdf.
Donlon, C.J., Minnett, P.J., Gentemann, C., Nightingale, T.J., Barton, I.J., Ward, B., & Murray, J. (2002). Toward improved validation of satellite sea surface skin temperature measurements for climate research. Journal of Climate 15, 353-369. doi: 10.1175/1520-0442(2002)015<0353:TIVOSS>2.0.CO;2
Donlon, C., Robinson, I.S., Reynolds, M., Wimmer, W., Fisher, G., Edwards, R., & Nightingale, T.J. (2008). An Infrared Sea Surface Temperature Autonomous Radiometer (ISAR) for Deployment aboard Volunteer Observing Ships (VOS). Journal of Atmospheric and Oceanic Technology 25, 93-113.
Freund, Y., Mason, L. (1999). The alternating decision tree learning algorithm. In: Proceeding of the Sixteenth International Conference on Machine Learning, Bled, Slovenia, 124-133. Available from http://perun.pmf.uns.ac.rs/radovanovic/dmsem/cd/install/Weka/doc/classifiers-papers/trees/ADTree/ atrees.pdf
Hanafin, J. A. (2001). On sea surface properties and characteristics in the infrared. Thesis (Ph.D.) University of Miami, 2002.; Publication Number: AAI3056632; ISBN: 9780493717869; Source: Dissertation Abstracts International, Volume: 63-06, Section: B, page: 2767.; 111 p.
Hanafin, J. A. and P. J. Minnett, (2002) Profiling temperature in the sea surface skin layer using FTIR measurements. Gas Transfer at Water Surfaces. edited by M. A. Donelan, W. M. Drennan, E. S. Saltzmann and R. Wanninkhof. American Geophysical Union Monograph 127, 161-166
Kilpatrick, K. A. Podestá, G.P., & Evans, R.H. (2001). Overview of the NOAA/NASA advanced very high resolution radiometer Pathfinder algorithm for sea surface temperature and associated matchup database. Journal of Geophysical Research. 106(C5):9179-9197. http://dx.doi.org/10.1029/1999JC000065
Kilpatrick, K. A., G. Podestá, S. Walsh, E. Williams, V. Halliwell, M. Szczodrak, O. B. Brown, P. J. Minnett, and R. Evans (2015). A decade of sea surface temperature from MODIS. Remote Sensing of Environment, 165, 27-41. http://dx.doi.org/10.1016/j.rse.2015.04.023
Kilpatrick, K.A., Podestá, G., Williams, E., Walsh, S., & Minnett, P.J. (2019). Alternating Decision Trees for Cloud Masking in MODIS and VIIRS NASA Sea Surface Temperature Products. Journal of Atmospheric and Oceanic Technology 36, 387-407. DOI: 10.1175/jtech-d-18-0103.1
Liang, X., & Ignatov, A. (2013). AVHRR, MODIS, and VIIRS radiometric stability and consistency in SST bands. Journal of Geophysical Research, 118(6), 3161–3171.http://dx.doi.org/10.1002/jgrc.20205
Liu, C., E. Freeman, E. C. Kent, B. Huang, H. M. Zhang, D. I. Berry, S. J. Worley, M. Ouellet, I. Gaboury, Z. Li, & V.F. Banzon (2019). ICOADS Drifting Buoy Data Recovery from BUFR and Its Impact on the OISST and ERSST. Poster presentation. American Meteorological Society 99th annual Meeting, Phoenix, January 6-10 2019. https://ams.confex.com/ams/2019Annual/webprogram/Paper352621.html
Minnett, P. J. (2010). The Validation of Sea Surface Temperature Retrievals from Spaceborne Infrared Radiometers. Oceanography from Space, revisited., V. Barale, J. F. R. Gower, and L. Alberotanza, Eds., Springer Science+Business Media B.V., 273-295.
Minnett, Peter J., and Gary K. Corlett (2012). A pathway to generating Climate Data Records of sea-surface temperature from satellite measurements. Deep Sea Research Part II: Topical Studies in Oceanography 77 (2012): 44-51.
Minnett, P. J., Evans, R. H., Podestá, G. P., & Kilpatrick, K. A. (2014). Sea-surface temperature from Suomi-NPP VIIRS: Algorithm development and uncertainty estimation. In Proceedings of SPIE - The International Society for Optical Engineering. (Vol. 9111). [91110C] SPIE. DOI: 10.1117/12.2053184
Minnett, P.J., Smith, M., & Ward, B. (2011). Measurements of the oceanic thermal skin effect. Deep Sea Research Part II: Topical Studies in Oceanography 58, 861-868. 10.1016/j.dsr2.2010.10.024
Pfahringer, B., G. Holmes and R. Kirkby (2001). Optimizing the Induction of Alternating Decision Trees. Proceedings of the Fifth Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. 2001, pp. 477-487. Available from http://www.cs.waikato.ac.nz/ml/publications/2001/pakdd2001.pdf
Rice, J.P., Butler, J.J., Johnson, B.C., Minnett, P.J., Maillet, K.A., Nightingale, T.J., Hook, S.J., Abtahi, A., Donlon, C.J., & Barton, I.J. (2004). The Miami2001 Infrared Radiometer Calibration and Intercomparison: 1. Laboratory Characterization of Blackbody Targets. Journal of Atmospheric and Oceanic Technology 21, 258-267.
Theocharous, E., Fox, N.P., Barker-Snook, I., Niclòs, R., Santos, V.G., Minnett, P.J., Göttsche, F.M., Poutier, L., Morgan, N., Nightingale, T., Wimmer, W., Høyer, J., Zhang, K., Yang, M., Guan, L., Arbelo, M., & Donlon, C.J. (2019). The 2016 CEOS Infrared Radiometer Comparison: Part II: Laboratory Comparison of Radiation Thermometers. Journal of Atmospheric and Oceanic Technology 36, 1079-1092. doi: 10.1175/jtech-d-18-0032.1
Vincent, R. (2019). The Case for a Single Channel Composite Arctic Sea Surface Temperature Algorithm. Remote Sens. 2019, 11, 2393.
Vincent, R.F., Marsden, R.F., Minnett, P.J., Creber, K.A.M., & Buckley, J.R. (2008a). Arctic Waters and Marginal Ice Zones: A Composite Arctic Sea Surface Temperature Algorithm using Satellite Thermal Data. Journal of Geophysical Research 113, C04021. doi: 10.1029/2007JC004353
Vincent, R.F., Marsden, R.F., Minnett, P.J., & Buckley, J.R. (2008b). Arctic Waters and Marginal Ice Zones: Part 2 - An Investigation of Arctic Atmospheric Infrared Absorption for AVHRR Sea Surface Temperature Estimates. Journal of Geophysical Research 113, C08044. doi: 10.1029/2007JC004354
Walton, C. C., Pichel, W. G., Sapper, J. F., and May, D. A. (1998). The development and operational application of nonlinear algorithms for the measurement of sea surface temperatures with the NOAA polar-orbiting environmental satellites, Journal of Geophysical Research, 103, 27,999-928,012.
Wong, E.W., & Minnett, P.J. (2016). Retrieval of the Ocean Skin Temperature Profiles from Measurements of Infrared Hyperspectral Radiometers - Part I: Derivation of an Algorithm. IEEE Transactions on Geoscience and Remote Sensing 54, 1879-1890. 10.1109/TGRS.2015.2483746
Wong, E.W., & Minnett, P.J. (2018). The Response of the Ocean Thermal Skin Layer to Variations in Incident Infrared Radiation. Journal of Geophysical Research, 123, 19. doi:10.1002/2017JC013351 Xu, F., & Ignatov, A. (2014). In situ SST Quality Monitor (iQuam). Journal of Atmospheric and Oceanic Technology 31, 164-180. doi: 10.1175/JTECH-D-13-00121.1